本文重心

在线性代数边界，矩阵的条款数（Condition Number）是一个至关迫切的看法。矩阵条款数示意了矩阵缱绻对于差错的明锐性，本文先容矩阵条款数在线性方程组求解中的运用。

例如

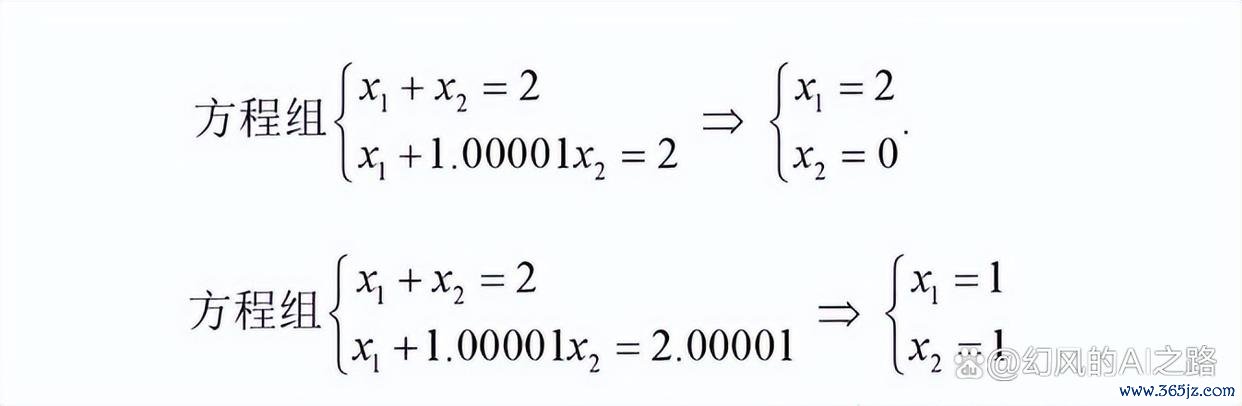
如图所示，现时有两个方程组，方程组只是是b不同，但是欧洲杯体育它们的成果却进出很大，为什么会出现这么的情况呢？咱们不错从矩阵条款数的角度来判断这个问题。

矩阵条款数

现时有一个矩阵AX=b,如若矩阵A的条款数过大，那么b的微弱改换就能引起解x较大的改换，数值安逸性差。那么若何缱绻矩阵的条款数呢？

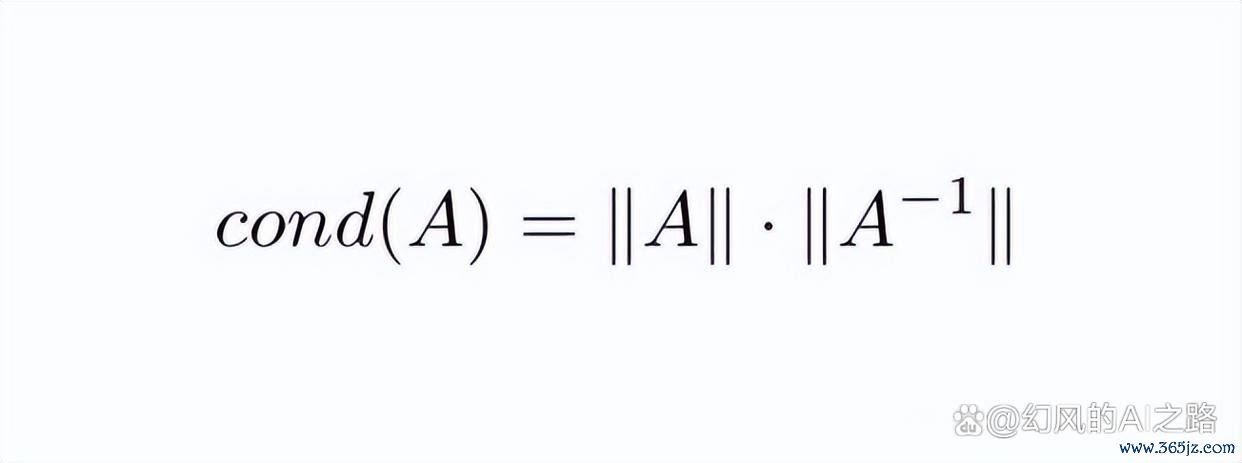
矩阵条款数的缱绻公式如图所示，它即是矩阵的范数乘以矩阵逆的范数。

在缱绻矩阵条款数时，不错遴选不同的范数来探讨矩阵的大小。以下是一些常见的缱绻才调：

1-范数条款数：使用矩阵A的1-范数和其逆矩阵A^(-1)的1-范数的乘积来缱绻。1-范数界说为矩阵列和的最大值。2-范数条款数：使用矩阵A的2-范数和其逆矩阵A^(-1)的2-范数的乘积来缱绻。2-范数（谱范数）界说为矩阵最大奇异值。无限范数条款数：使用矩阵A的无限范数和其逆矩阵A^(-1)的无限范数的乘积来缱绻。无限范数界说为矩阵行和的最大值。

矩阵条款数的性质

安逸性与精度：条款数是探讨矩阵缱绻安逸性和精度的迫切办法。当条款数较小时，矩阵缱绻相对安逸，差错不易被放大；而当条款数较大时，矩阵缱绻则变得不安逸，微弱的差错也可能导致缱绻成果的显赫偏离。

病态与良态：条款数也不错看作是对矩阵“病态”进度的一种度量。如若条款数接近1，则矩阵是“良态”的；如若条款数很大，则矩阵是“病态”的。病态矩阵在数值缱绻中每每会导致较大的差错。矩阵的条款数一定是大于即是1的，咱们不错通过底下的施行来详情：

特征值与奇异值：对于正门径阵（如对称矩阵或正交矩阵），在2-范数下的条款数不错示意为最大特征值与最小特征值的王人备值之比。此外，矩阵的条款数也不错通过其奇异值来界说和缱绻。

实例分析

以下是一个对于矩阵条款数的实例分析，以进一步分解其在实质运用中的迫切性。

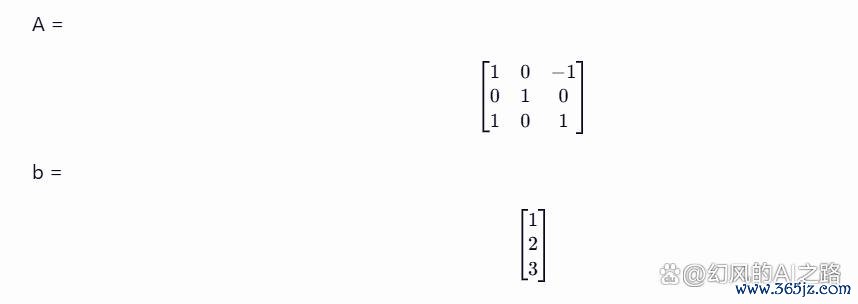
假定有一个线性方程组Ax=b，其中A是一个3x3的矩阵，b是一个3维向量。现时，咱们缱绻矩阵A的条款数，并分析其对解x的影响。

给定矩阵A和向量b如下：

以2-范数为例）：

cond(A, 2) = 1.4142

由于条款数较小（接近1），咱们不错以为矩阵A是良态的。因此，在求解线性方程组Ax=b时，咱们不错生机赢得相对安逸的解。实质上，使用高斯消元法或LU分解等才调求解该方程组，不错赢得精准的解x。

但是，如若咱们对矩阵A进行微弱的扰动（例如改换其中一个元素的微弱值），并从头缱绻条款数，可能会发现条款数显赫加多。这意味着扰动后的矩阵可能变得病态，导致求解线性方程组时的差错增大。因此，在实质运用中，咱们需要热心矩阵的条款数以评估其安逸性和精度。